n-Riemann invariant is a function of the solution \(q\) whose values are invariant along any integral curve of the eigenvector \(r^n\), which is the \(n^{th}\) eigenvector of the system Jacobian.¹

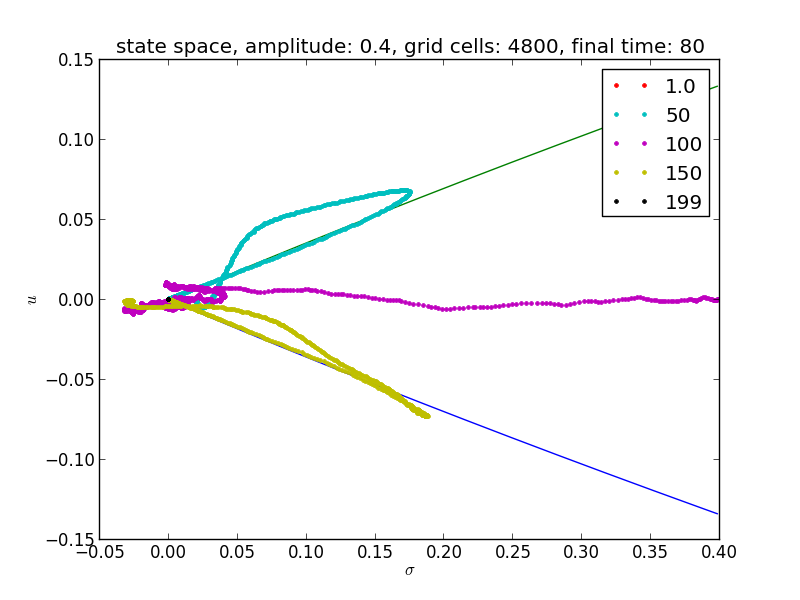
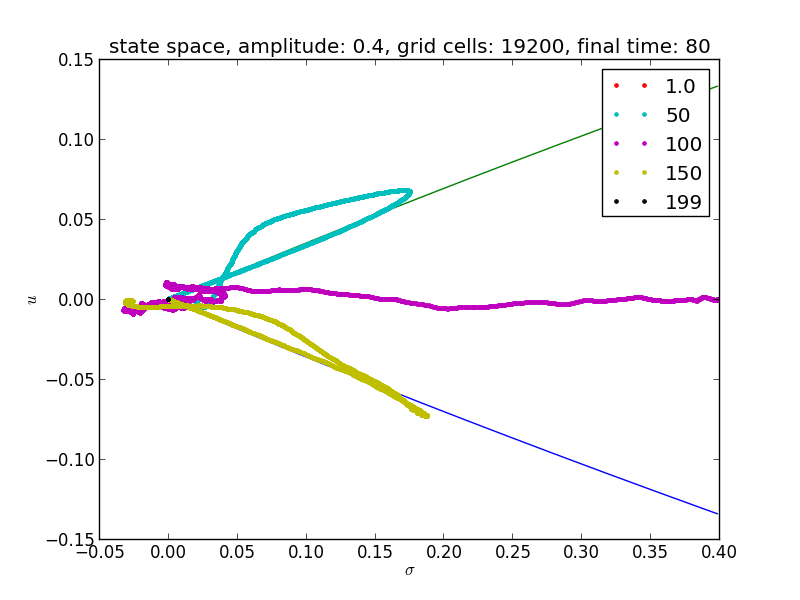
Following the approach of Leveque and Yong paper ², we are showing some results for the phase plane of nonlinear elastic waves equation propagating in random media.

The medium is piece-wise constant with \(K=\rho\) which take uniformly distributed random values from 1 to 5.

We are showing also the integral curves of the corresponding simple homogenized system which are:

\[u = \pm \frac{2}{Z_0} (1-\sqrt{\sigma+1})\] where \[Z_0 = \sqrt{\hat{K}\bar{\rho}}\]

Here \(\delta=0.5\) and the period length is one.

1

We show the results for two different resolutions

The initial solution: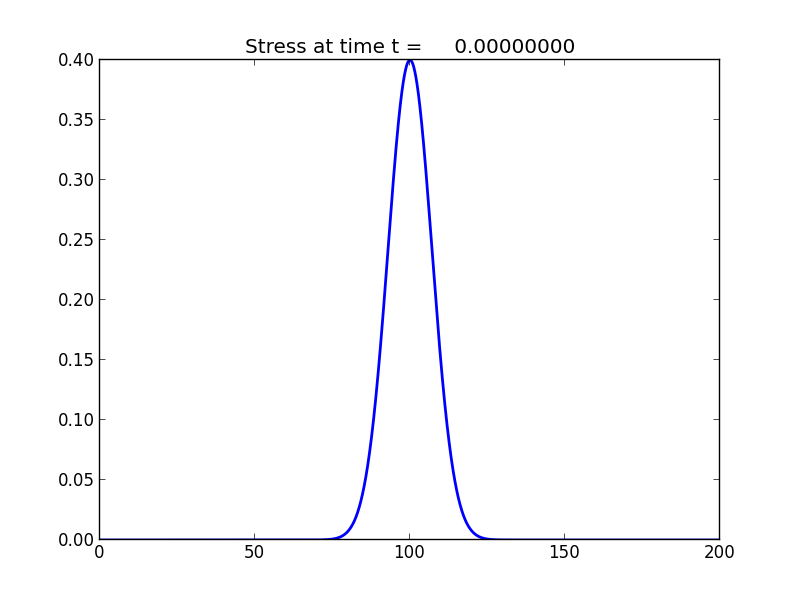

The final solution: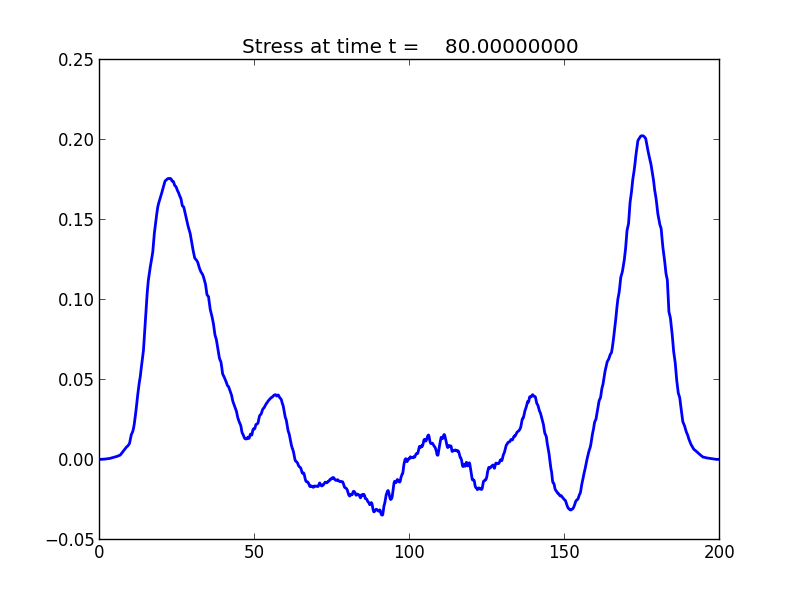

2

This is the same experiment but for different random variable seed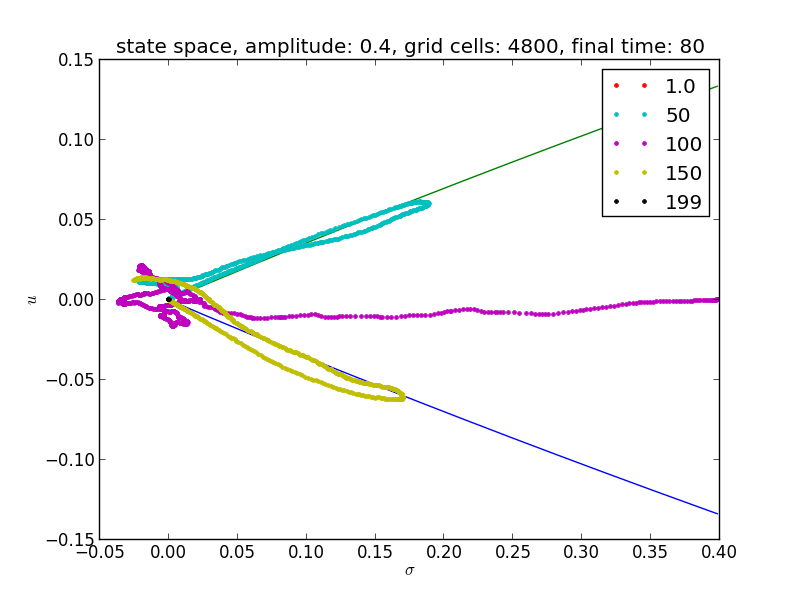

3

Medium realization same as (1) and some gauges are in the mid of the layer

4

And for larger amplitude:

5

similar to (4) but some gauges corresponds to the mid of one of the layers