nwhm/group and phase velocity
In the section regarding the instability of the homogenized equations, here, we considered the combined system of homogenized equations up to \(O(\delta^2)\) for 1D z-dispersion. Here is the equation again:
\(K_h^{-1}\rho_m\sigma_{tt}-\sigma_{xx}=\delta^2\left(\alpha_1+\gamma_1\right)\sigma_{xxxx}+O\left(\delta^4\right),\)
We also derived the group velocity, which is:
\(v_g=\frac{\partial\omega}{\partial k}=\hat{c}\frac{1-2\delta^2(\alpha_1+\gamma_1)k^2}{\sqrt{1-\delta^2(\alpha_1+\gamma_1)k^2}}\)
The idea is now to obtain stationary macroscopic solutions; i.e., a solution whose group velocity is \(v_g=0\). This is clearly obtain when:
\(k^2=\frac{1}{2\delta^2(\alpha_1+\gamma_1)}\)
If we start with a monochromatic wave with this frequency, we should get a standing (or stationary) wave.
Consider the following material properties:
\(\begin{eqnarray*} K_A &=& 4; &\rho_A &=& 4, \\ K_B &=& 1; &\rho_B &=& 1. \end{eqnarray*}\)
Then, to achieve standing waves we need \(k\approx 5.7735\). The following is an animation of that situation. For stability reasons (of the spectral simulations) I have to increase the total length so I get more than one period, this shouldn’t be a problem for the FV simulations.
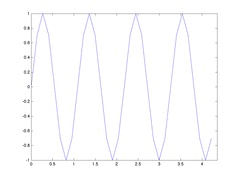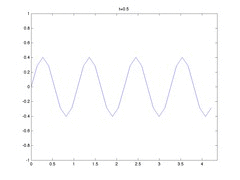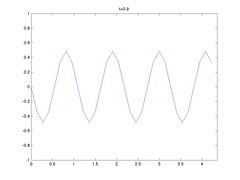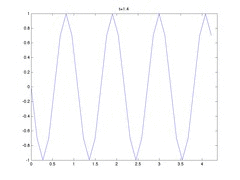
NOTES:
- This is based on an approximation of the homogenized equations (I dropped a term of \(O(\delta^4)\)). I have worked out the wave number if I don’t drop out such term and I got:
\(k^2=\frac{(\alpha_1+\gamma_1)\pm\sqrt{(\alpha_1+\gamma_1)^2-3\alpha_1\gamma_1}}{3\delta^2\alpha_1\gamma_1},\)
which for the parameters above gives \(k_-\approx 22.2222...\) and \(k_+\approx 66.6666...\). They are obviously multiple of each other. We have to understand that both expressions for \(k\) are approximations; obviously, the second one is better.
Now, it is obvious that \(22.222 * 3 = 66.666\). If we include other correction in the homogenized equations, we will get other 2 zeros so we would get a total of 4 values of \(k\) that make \(v_g=0\). Including more and more corrections would introduce more and more zeros. If these zeros are indeed multiple of each other, then we can think of them as harmonics. We can corroborate this using the homogenized equation in LY that includes terms of \(O(\delta^4)\).
Now, the idea we have so far is that these values of \(k\) are indicating edge points of band gaps; i.e., regimes of wave numbers that can’t be propagated in the medium.
We still have to investigate the phase velocity.
