Effective Lax-Entropy condition on C-dispersive media

At first we proposed the critical sound speed from the right state was going to be the maximum of the sound speed; i.e.,

\(\begin{align} s_{eff}^{(R)}>\max (c_A(\sigma_r), c_B(\sigma_r)); \end{align} \) however, it is easy to verify this is wrong. Based on some experiments, we propose:

\(\begin{align} s_{eff}^{(R)}>c_m(\sigma_r):=\int_\Omega\sqrt{\frac{\sigma_r^\prime (x)}{\rho(x)}} dx; \end{align} \) i.e., the critical sound speed is the arithmetic average. Here we try to corroborate this hypothesis via numerical experiments.

CONSTANT IMPEDANCE: \(Z=1\)

We start considering a heterogeneous medium that is purely c-dispersive (i.e., no z-dispersion) and increase the speed by changing the strength of the initial condition. We consider two experiments. First we start with an smooth initial condition that is close to become a shock. The idea here is to determine at which point (in the speed of propagation) the solution develops shocks. The second experiment consists on starting with a right-going shock and determine at which point the shock gets regularized.

The material parameters are chosen as follows:

\(\begin{align} K_A &=\frac{1+r}{2r}; &\rho_A &= \frac{2r}{1+r}, \\ K_B &=\frac{1+r}{2}; &\rho_B &= \frac{2}{1+r}. \end{align}\)

where \(r=\frac{c_B}{c_A}\). This assures:

\(\begin{align} z_A &=1, & z_B = 1, \\ c_h &=1. \end{align}\)

Therefore, the medium is purely c-dispersive. Later we consider more general scenarios.

Starting with smooth initial conditions

First we start with an smooth initial condition given by:

\(\begin{align} \sigma=\frac{\sigma_l+\sigma_r}{2}-\frac{\sigma_l-\sigma_r}{2}\tanh(x-5), \end{align} \)

and the velocities are such that the initial condition is aligned with the right-going eigenvector (of the linearized flux Jacobian); this produces an almost purely right-going wave. Note that the initial condition for \(\sigma\) is infinitely smooth. The following pictures show the initial condition and the solution at \(t=3\) and \(t=6\) for a homogeneous medium and a medium such that \(c_B/c_A=3\).

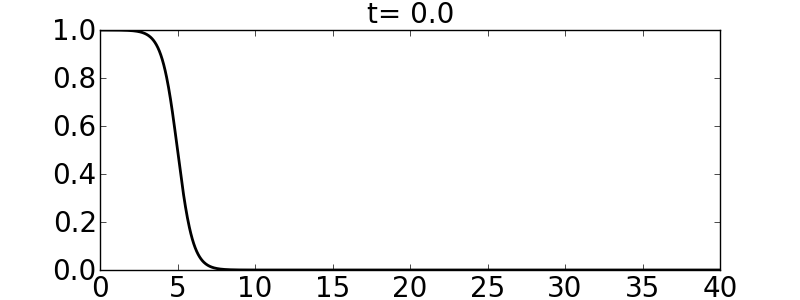
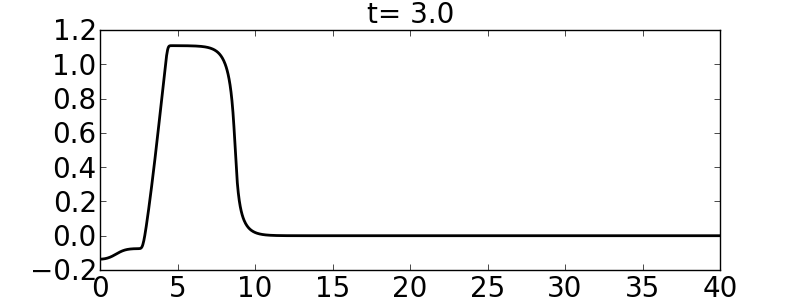
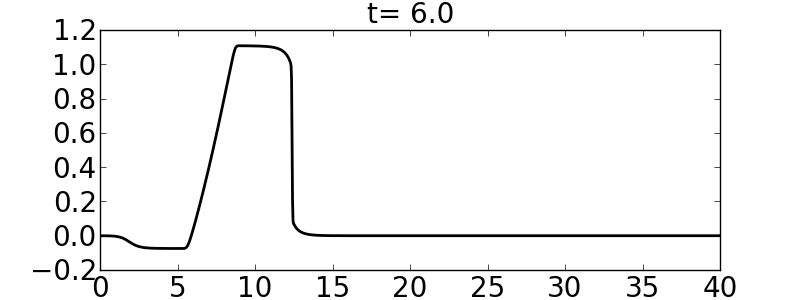
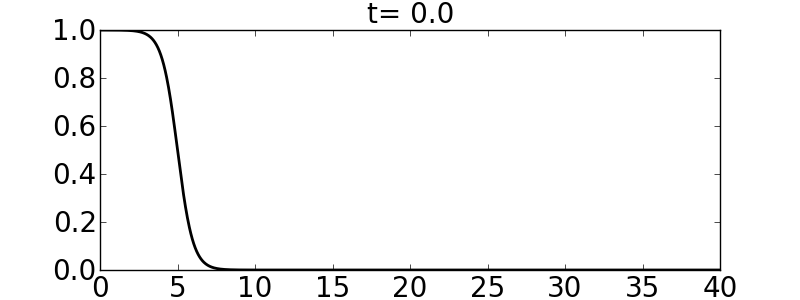
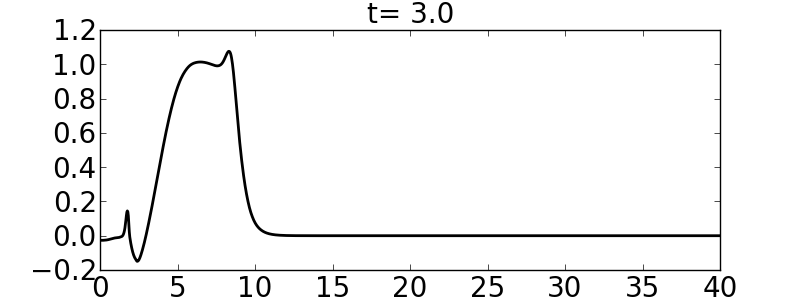
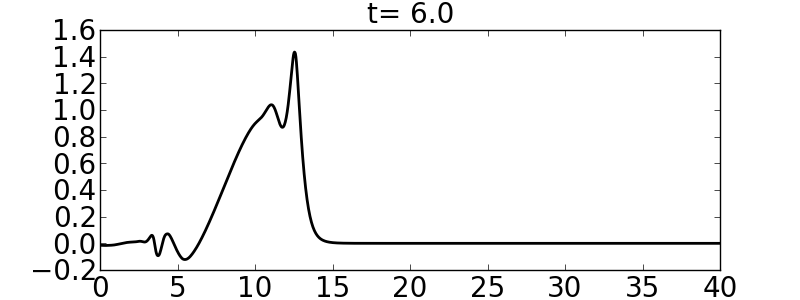
Final time=20

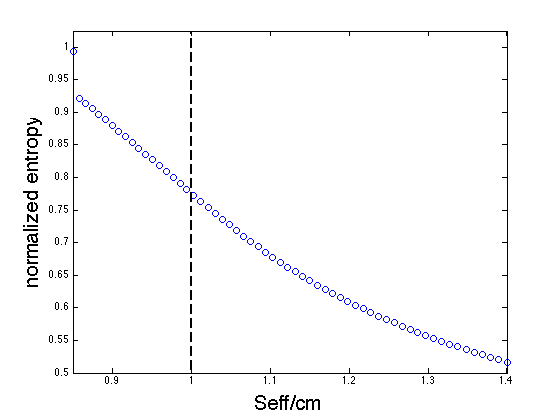
Now we consider a domain from \((x,y)=[0,40]\times [0,1]\), impose reflecting boundary conditions at the left boundary, periodic in the \(y\)-direction and outflow at the right. We consider a material with material properties: \(K_A=2/3\), \(\rho_A=3/2\), \(K_B=2\) and \(\rho_B=1/2\); this yields to \(c_B/c_A=3\). We choose \(\sigma_r=0\) and run different experiments changing only \(\sigma_l\). In this setting \(c_m=\frac{1}{2}(c_A+c_B)=\frac{4}{3}\) is fixed and \(s_{eff}=\sqrt{\frac{K_h}{\rho_h}}\sqrt{\frac{\sigma_l}{\log{(\sigma_l+1)}}}\) is monotonically increasing. Note that as \(\sigma_l\rightarrow 0\), \(s_{eff}\rightarrow \sqrt{\frac{K_h}{\rho_h}}\approx 1.1547\). Then, by increasing \(\sigma_l\), starting close to zero, we can control \(s_{eff}\) relative to \(c_m\). We run 30 experiments up to \(t=20\) for values of \(\sigma_l\) such that \(s_{eff}/c_m\) changes uniformly from \([1.175/c_m, 1.75/c_m] = [0.88125, 1.3125]\). For each experiment we plot (in the \(y\)-axis) the entropy at \(t=20\) relative to the entropy at \(t=0\) vs the corresponding \(s_{eff}/c_m\) (in the \(x\)-axis).

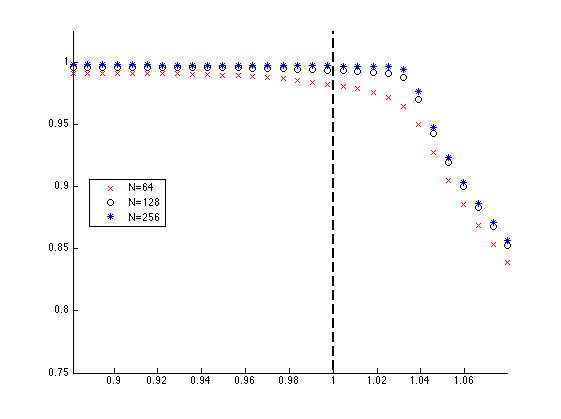
If the solution propagates without shock formation, the entropy remains constant, so the relative entropy remains close to one (any loss in entropy is due to numerical dissipation). If the initial solution evolves into a shock, the entropy starts to get lost. It is evident at this point (in time) there are no shocks formed for values such that \(s_{eff}<c_m\); i.e., the solution remains smooth. When \(s_{eff}\) is slightly larger than \(c_m\) there seems to be no shock; however, as we increase \(s_{eff}\) shocks clearly start to occur. In particular, it appears that for the fifth point after \(c_m\) (vertical dashed line) there is already a shock; this point is about \(3\%\) larger than \(c_m\). For the points to the left, a more careful study is necessary. In particular, a shock may occur in later times so we have to consider later times (and therefore larger domains).

Different final times

Now we consider three points to the left of \(c_m\) and six to the right and run the simulation up to different final times \(T=[20, 40, 60, 80, 100]\). We perform the experiment for two different resolutions of \(Nx=128\) (left) and \(Nx=256\)(right).

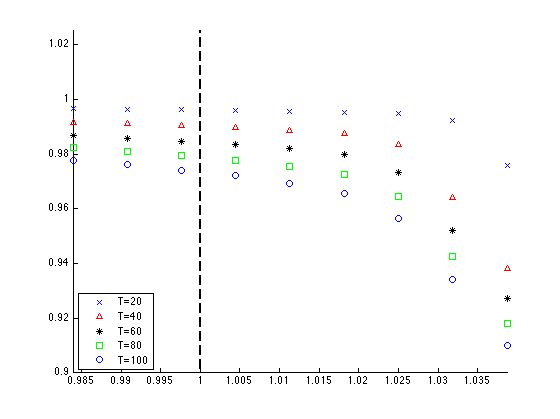
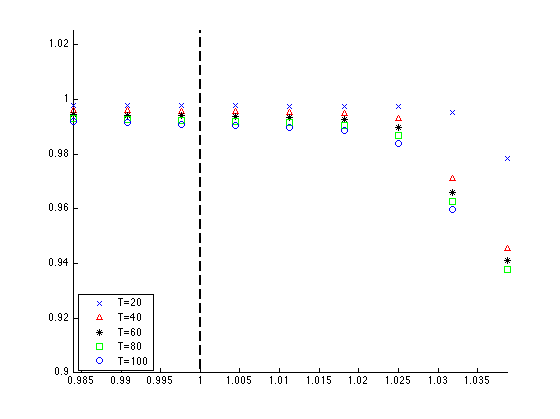
Now it appears that a shock is present starting around the 3rd or 4th point, which are about \(2\%\) away from \(c_m\).

Starting with shocks

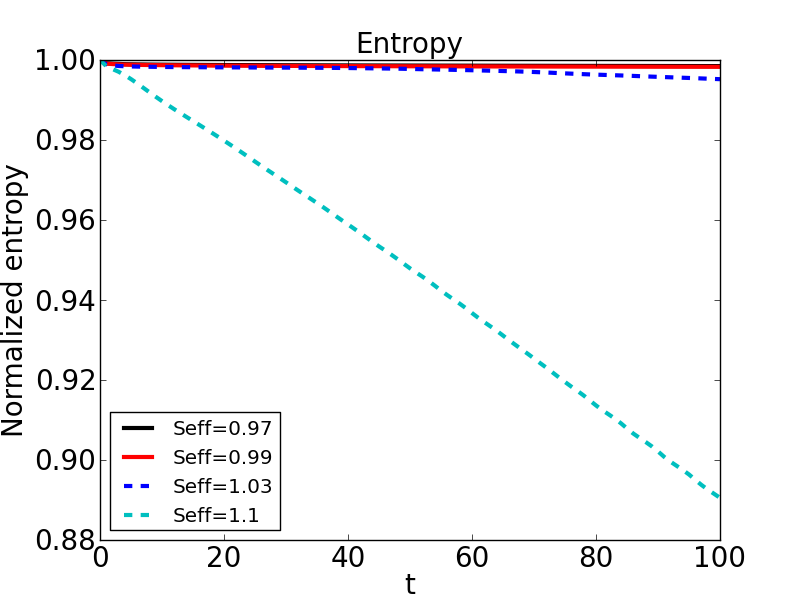
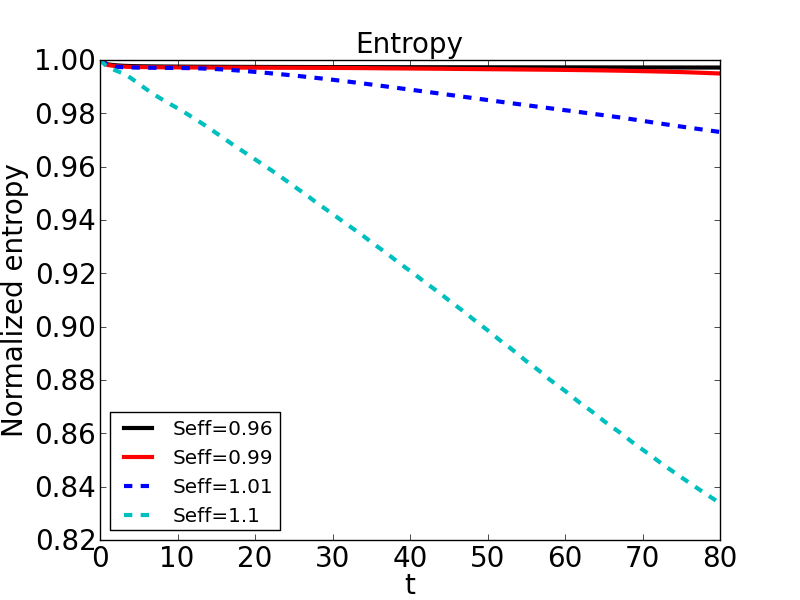
In this experiment we start with an effective right-going shock, see the section about effective R-H conditions. We run experiments using different media, all purely c-dispersive, and measure the relative loss in entropy. In the following pictures we show the results for \(c_B/c_A=2\) (left) and \(c_B/c_A=4\) (right). Here, we use the convention in KL and define:

\(\begin{align} S_{eff}:=\frac{s_{eff}}{c_m}, \end{align} \)

where \(s_{eff}\) is the shock speed and \(c_m(\sigma_r)\), the critical characteristic speed, is the arithmetic average. These results effectively corroborate our theory. On purely c-dispersive media, an stable shock propagates faster than the arithmetic average of the sound speed at the right state of the shock. Now, we try to extend this to more general settings; i.e., not only purely c-dispersive media.

NON-CONSTANT IMPEDANCE

Previously we considered a fixed heterogeneous material and consider \(\sigma_r=0\) and different values for \(\sigma_l\). Now we consider a more general setting where \(K_A=\rho_A=1\) and we change \(K_B\), \(\rho_B\) and \(\sigma_l\) while \(\sigma_r\) is fixed. NOTE: \(K_A\) and \(\rho_A\) can be fixed without loss of generality, this is shown here.

We consider \(\rho_A=K_A=1\) and change \(\rho_B\), \(K_B\) and \(\sigma_l\) so that \(s_{eff}/c_m\) is (almost) uniformly distributed. We plot the normalized entropy lost (y-axis) vs \(s_{eff}/c_m\) (x-axis). It is clear that the condition that \(s_{eff}>c_m\) leads to stable shocks is not true anymore.