nwhm/cZ-dispersion

Considering a striped media, say horizontally striped, one may obtain c- and Z- dispersion by choosing the coefficients so that \(Z_A\neq Z_B\) and \(c_A\neq c_B\). This would introduce c-dispersion in \(x\) and Z-dispersion in \(y\). An example of such setting is:

\(\begin{eqnarray*} K_A &=& 1; &\rho_A &=& 1, \\ K_B &=& 16; &\rho_B &=& 1. \end{eqnarray*}\)

Then,

\(\begin{eqnarray*} Z_A &=& 1; &c_A &=& 1, \\ Z_B &=& 4; &c_B &=& 4. \end{eqnarray*}\)

The homogenized equations for these set of parameters is:

\(\begin{eqnarray*} K_h^{-1}\sigma_t-\left(\sigma+1\right)\left(u_x+v_y\right) & = & \alpha_1\left[\left(\sigma+1\right)\left(u_{xyy}+v_{yyy}\right)+2\sigma_y\left(u_{xy}+v_{yy}\right)\right]\\ & & +\alpha_2\left[\left(\sigma+1\right)\left(u_{xxx}+v_{xxy}\right)+2\sigma_x\left(u_{xx}+v_{xy}\right)\right]\\ \rho_h u_t-\sigma_x & = & 0,\\ \rho_m v_t-\sigma_y & = & 0, \end{eqnarray*}\)

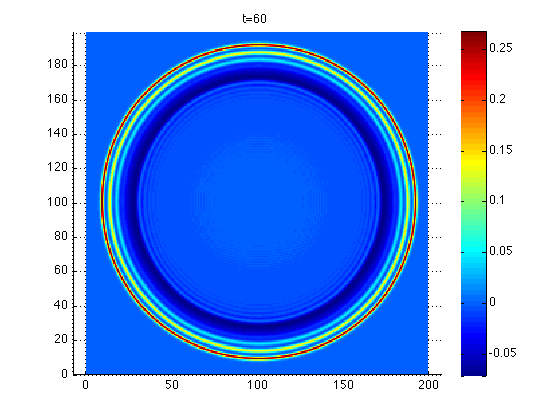
with \(\alpha_1=\alpha_2=\frac{75}{4624}\). We can see that for this set of parameters the dispersion is symmetric in \(x\) and \(y\). Therefore, the solution is symmetric so we obtain circular solitary waves, which we couldn’t get in the paper regarding 2D stegotons in checkerboard media.

As David explained this means we have an isotropic behavior in a medium totally anisotropic (horizontally striped medium). These results are just using the homogenized equations so we can’t conclude yet the original variable coefficient PDE is isotropic for this set of parameters (we just know it is up to some order). A FV simulation may give an indication about this. I will run this simulation in the coming days.

Here is a plot of the pseudo-spectral simulation of the homogenized equations.

It would be nice to run another case where the propagation is not isotropic, just to show the contrast.