nwhm/Shocks in c-dispersive media

Jump condition and right-going shock

Let’s start considering the original wave equation in 2D:

\(\begin{eqnarray*} q_t+f(q)_x+g(q)_y=0 \end{eqnarray*}\)

where \(q=[\epsilon, m^x, m^y]^T\), \(f(q)=[-\rho^{-1}m^x, -\sigma, 0]^T\) and \(g(q)=[-\rho^{-1}m^y, 0, -\sigma]^T\), where \(m^x\) and \(m^y\) denote the momentum in \(x\) and \(y\) respectively. If we assume the solution is homogeneous in \(y\) and consider a 1D Riemann Problem in \(x\) where the interface is given by a shock in \(x\) one can derive the jump conditions to be \([f]=s[q]\), which for this particular problem gives:

\(\begin{eqnarray*} -\rho [m^x]&=&s[\epsilon],\\ -[\sigma]&=&s[m^x],\\ 0&=&s[m^y]. \end{eqnarray*}\)

If we assume \(s\neq 0\), a non-stationary shock, then \([m^y]=0\) so this shock in \(x\) don’t carry discontinuities in the momentum in \(y\). Solving for \(s\neq 0\) yields:

\(\begin{eqnarray*} s=\pm \sqrt\frac{[\sigma]}{\rho [\epsilon]}. \end{eqnarray*}\)

By assuming the right state vanishes; i.e., \(\epsilon_r=u_r=0\) and considering the positive shock speed, we get the conditions for having a right going shock:

\(\begin{equation} u_l=-\sqrt{\frac{\sigma_l\log(\sigma_l+1)}{\rho K}}, \end{equation}\)

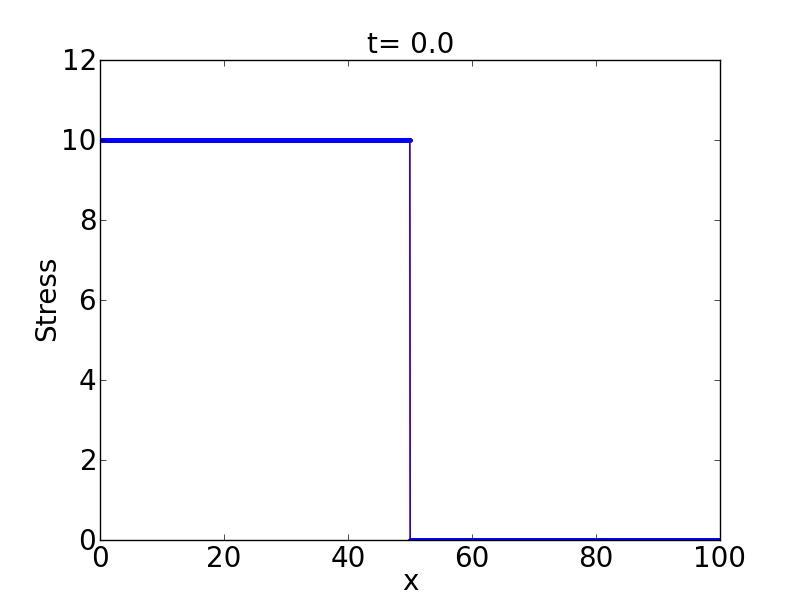
and we consider \(v_l=v_r=0\). This is all valid if we have a solution homogeneous in \(y\); for instance, in each material by itself. However, this is not true when the coefficients are changing in \(y\). Even if we have no shocks in \(y\), the solution is changing in \(y\) so \(g(q)_y\neq 0\). Nevertheless, it does give an almost right going shock, which is good enough for what we need, study the stability of a shock in c-dispersive media. The following figures show an initial condition for sigma and the solution at \(t=5\). One can see the wave is not purely right going.

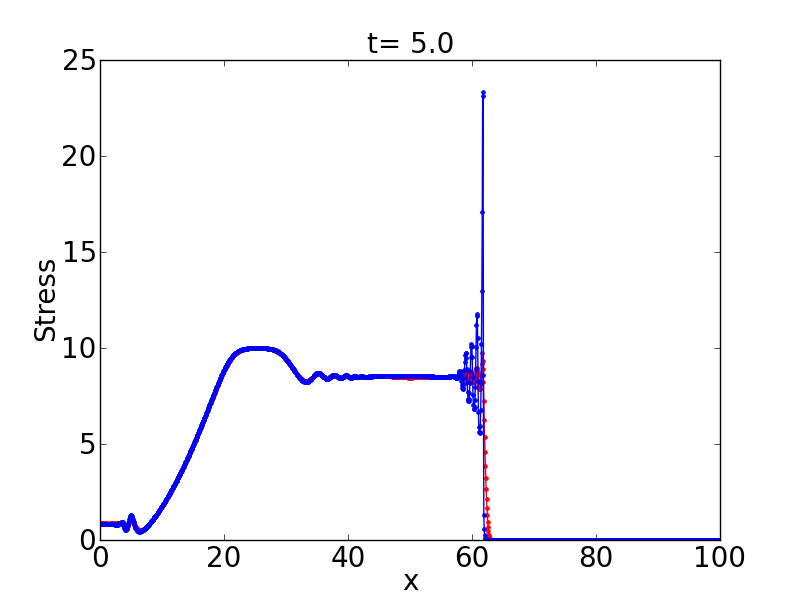
If we consider \(\rho_h\) and \(K_h\) into the equation for \(u_l\) we get the following stress at \(t=5\). It is evident this is a better choice for having a right going shock. We use this from now on.

Material parameters

The material parameters are chosen as follows:

\(\begin{eqnarray*} K_A &=& \frac{1+r}{2r}; &\rho_A &=& \frac{2r}{1+r}, \\ K_B &=& \frac{1+r}{2}; &\rho_B &=& \frac{2}{1+r}. \end{eqnarray*}\)

where \(r=\frac{c_B}{c_A}\). This assures:

\(\begin{eqnarray*} z_A &=& z_B = 1, \\ c_h &=& 1. \end{eqnarray*}\)

It is convenient to always use \(r\geq 1\) so that \(c_B\geq c_A\) is always true. Since \(c_h=1\) we have that \(c_A\) and \(c_B\) are relatively small, which is nice to avoid having to consider extremely large domains. The effective sound speed \(c_{eff}\) is given by:

\(\begin{equation*} c_{eff}=\frac{1+r}{2\sqrt{r}}, \end{equation*}\)

and obviously \(c_A\leq c_{eff} \leq c_B\).

Speed of the shock

Based on the homogenized equations and on the K&L paper about dynamics od shocks in z-media, one may expect the speed of the shock in c-media is given by:

\(\begin{eqnarray*} s_{eff}=\pm \sqrt{\hat{\left(\frac{[\sigma]}{[\epsilon]}\right)}\frac{1}{\rho_h}}=\pm \sqrt{\frac{K_h\sigma_l}{\rho_h\log{(\sigma_l+1)}}}=\pm c_{eff}\sqrt{\frac{\sigma_l}{\log{(\sigma_l+1)}}}, \end{eqnarray*}\)

this is nicely corroborated by experiments. I have run several simulations with right-going shocks and measure the speed of the maximum point and compare this measurement with \(s_{eff}\) getting very good agreement. I am thinking about doing a convergence study and see if the speed of my measurement converge to \(s_{eff}\) as the grid is refined. Off course, there is a \(\Delta x\) error introduced by locating the max point so one can expect first order convergence.

Condition for stable shocks

Homogeneous media

If the material is homogeneous a right-going shock occurs when the characteristics corresponding to the positive eigenvalue impinge. These characteristics are given by:

\(\begin{equation*} \lambda_2=\sqrt{\frac{\sigma_\epsilon}{\rho}}=\sqrt{\frac{K(\sigma+1)}{\rho}}=c\sqrt{\sigma+1}. \end{equation*}\)

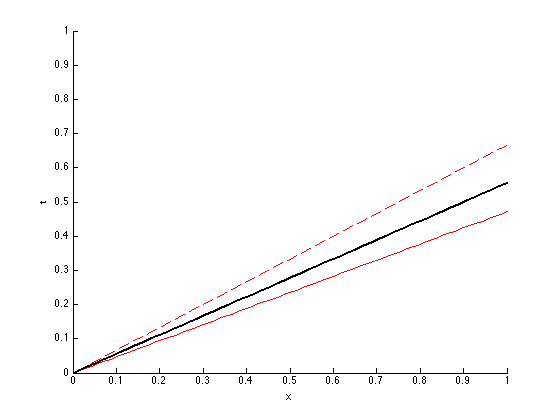
Considering the right state is zero we get a shock in the homogeneous case always that \(\sigma_l>0\). The following is a figure of the x-t plane of that situation. The solid red line is a characteristic coming from the left and impinging in a characteristic form the right, which is the dashed red line. The corresponding shock is shown in black.

Heterogeneous c-media

Now let’s consider the heterogeneous c-media. The following is a figure of the characteristics for each material. The characteristics from the left state are in solid and the ones form the right state are dashed. Material A and B are represented by blue and red colors respectively. The shock, if it exists, must be somewhere in the middle.

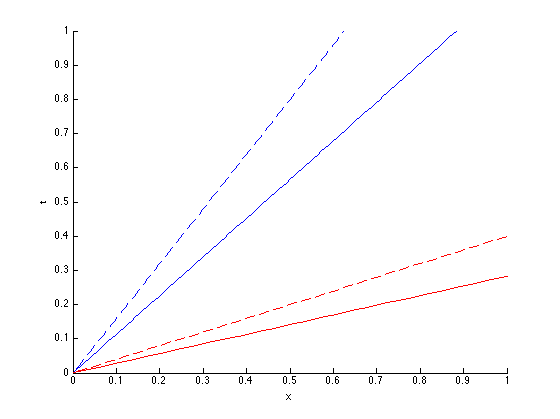
The characteristics (from left to right) are given by:

\(\begin{eqnarray*} \lambda_{2,A}^{(R)}&=&c_A=\frac{1+r}{2r}, \\ \lambda_{2,A}^{(L)}&=&c_A\sqrt{\sigma_l+1}=\frac{1+r}{2r}\sqrt{\sigma_l+1}, \\ \lambda_{2,B}^{(R)}&=&c_B=\frac{1+r}{2}, \\ \lambda_{2,B}^{(L)}&=&c_B\sqrt{\sigma_l+1}=\frac{1+r}{2}\sqrt{\sigma_l+1}, \\ \end{eqnarray*}\)

and the shock is given by:

\(\begin{equation*} s_{eff}=c_{eff}\sqrt{\frac{\sigma_l}{\log(\sigma_l+1)}}=\frac{1+r}{2\sqrt{r}}\sqrt{\frac{\sigma_l}{\log(\sigma_l+1)}} \end{equation*}\)